Discussion Forum

Let  $F_{1}(x_{1},0)$ and $F_{2}(x_{2},0)$  , for  $x_{1}<0$ and $x_{2}>0$ , be the foci of the ellipise $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ . Suppose a parabola  having vertex at the origin and focus at $F_{2}$ intersects the  ellipse  at the point M in the first quadrant and at point N  in the fourth quadrant

The orthocentre of  $\triangle F_{1}MN$ is 

Answer:

Explanation:

Here,  $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$             ..........(i)

 has foci (± ae,0)

  where ,   $a^{2}e^{2}=a^{2}-b^{2}\Rightarrow a^{2}e^{2}=9-8$

   $\Rightarrow$  ae=± 1, i.e.   $F_{1}.F_{2}=(\pm1,0)$

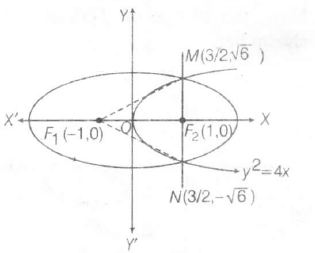
Equation of parabola having vertex  O(0,0) and   $F_{2}(1,0)$    (as $x_{2}>0$)

                                             $y^{2}=4x$             ........(ii)

On solving   $\frac{x^{2}}{9}+\frac{y^{2}}{8}=1$ and  $y^{2}=4x$ , we get

$x=\frac{3}{2}$ and  $y=\pm\sqrt{6}$

   Equation of altitude through M on NF₁ is

 $\frac{y-\sqrt{6}}{x-3/2}=\frac{5}{2\sqrt{6}}$

$\Rightarrow (y-\sqrt{6})=\frac{5}{2\sqrt{6}}(x-3/2)$         ............(iii)

and equation of altitude through

                          F₁   is y=0               ........(iv)

 On solving Eqs. (iii) and (iv), we get    $(-\frac{9}{10},0)$  as orthocentre.