Discussion Forum

Let P be the point on the parabola  $y^{2}=4x$ , which is at the shortest distance from the centre S of the circle .$x^{2}+y^{2}-4x+16y+64=0$. Let Q be the point on the circle dividing the line segment  SP internally. Then, 

Answer:

Explanation:

Tangent  to $y^{2}=4x$  at  $(t^{2},2t)$ is 

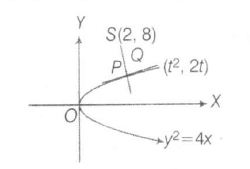
$y(2t)=2(x+t^{2})$

$\Rightarrow$              $yt=x+t^{2}$          ...........(i)

 Equation of normal  at $P(t^{2},2t)$  is

   $y+tx=2t+t^{3}$

 since, normal at P passes through centre of circle S (2,8).

$\therefore  8+2t=2t+t^{3}\Rightarrow t=2, i.e, P(4,4)$

 [Since, shortest distance between two curves lie along their common normal and the common  normal will pass through the centre of circle ]

$\therefore  SP=\sqrt{(4-2)^{2}+(4-8)^{2}}=2\sqrt{5}$

  $\therefore$ Option (a) is correct.

 Also, SQ=2

$\therefore   PQ=SP-SQ=2\sqrt{5}-2$

Thus,   $\frac{SQ}{QP}=\frac{1}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{4}$

    $\therefore$  Option (b) is incorrect.

 Now, x- intercept of normal is 

                    $x=2+2^{2}=6$

 $\therefore$  Option (c) is correct.

  Slope of tangent= $\frac{1}{t}=\frac{1}{2}$

$\therefore$  Option (d) is incorrect