Answer:
Option B,C,D
Explanation:
(a) Nearest neighbour in the topmost layer of ccp structure is 9 thus, incorrect
(b) Packing efficiency is 74% thus, correct
(c) Tetrahedral voids=2
Octahedral voids= 1 per atom thus, correct.
(d) Edge length,
$a=\frac{4}{\sqrt{2}}r=2\sqrt{2}r$
thus, correct explanation
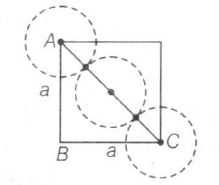
Edge length=a, Radius=r
$AC^{2}=AB^{2}+BC^{2}$
$(4r)^{2}=a^{2}+a^{2}=2a^{2}$
$4r=\sqrt{2}a\Rightarrow r=\frac{\sqrt{2}}{4}a=\frac{a}{2\sqrt{2}}$
$\therefore a=2\sqrt{2}r$
In ccp structure, the number of sphere is 4,
Hence , volume of 4 spheres= $4(\frac{4}{3}\pi r^{3})$
Total volume of unit cell= $a^{3}=(2\sqrt{2}r)^{3}$
% of packing efficiency= $\frac{volume. of 4 spheres}{ volume .of unit cell}$
= $\frac{4(\frac{4}{3}\pi r^{3})}{(2(\sqrt{2}r))^{3}}\times100=74.05$%= 74%
