Discussion Forum

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non- inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of a non-inertial frame of reference. The relationship  between the force  $\overrightarrow{F}_{rot}$  experienced by a particle of mass m moving on the  rotating disc and the force  $\overrightarrow{F}_{in}$ experienced by the particle in an inertial frame of reference is,

$\overrightarrow{F}_{rot}= \overrightarrow{F_{in}}+2m(\overrightarrow{v}_{rot}\times \overrightarrow{ \omega})+ m(\overrightarrow{\omega}\times \overrightarrow{r})\times\overrightarrow{\omega}$

  where, V_rot is the velocity of the particle in the rotating  frame of reference and r is the position vector of the particle with respect to center of the disc

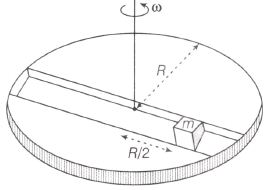
Now, consider a smooth slot along a diameter of a disc of radius R  rotating counter-clockwise with a constant angular speed ω about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and Z-axis along the rotation axis($(\omega =\omega\hat{k})$. A small block of mass m is gently placed in the slot at $r=(\frac{R}{2})\hat{i}$ at t=0 and is constrained to move only along the slot

The net reaction  of the disc  on the block is

Answer:

Explanation:

$F_{rot}=F_{in}+2m(v_{rot}\hat{i})\times \omega \hat{k}+m(\omega \hat{k}\times r\hat{i})\times \omega \hat{k}$

$mr\omega^{2}\hat{i}=F_{in}+2 mv_{rot}\omega (-\hat{j)}+m\omega^{2}r\hat{j}$

$F_{in}=2mv_{r}\omega \hat{j}$

$r=\frac{R}{4}[e^{\omega t}+e^{-\omega t}]$

 $\frac{\text{d}r}{\text{d}t}=v_{r}=\frac{R}{4}[\omega e^{\omega t}- \omega e^{-\omega t}]$

$F_{in}=2m\frac{R\omega}{4}[e^{\omega t}-e^{-\omega t}]w\hat{j}$

 $F_{in}=\frac{mR\omega^{2}}{2}[e^{\omega t}-e^{-\omega t}]\hat{j}$

Also , reaction  is due to disc surface , then

 $F_{reaction}=\frac{mR\omega^{2}}{2}[e^{\omega t}-e^{-\omega t}]\hat{j}+mg\hat{k}$