Discussion Forum

In the circuit shown below, the key is  pressed at time t=0, Which of the following statement(s) is (are)  true?

Answer:

Explanation:

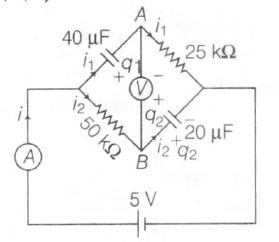
Just after pressing key,

  5-25000i₁ =0

5-50000 i₂ =0

 ( As charge in both capacitors =0)

$\Rightarrow i_{1}=0.2mA\Rightarrow i_{2}=0.1mA$

And  $V_{B}+25000i_{1}=V_{A}$

$\Rightarrow V_{B}-V_{A}=-5V$

After a long time , i₁  and i₂ =0 ( steady state)

$\Rightarrow 5-\frac{q_{1}}{40}=0\Rightarrow q_{1}=200\mu C$

and  $5-\frac{q_{2}}{20}=0\Rightarrow q_{2}=100\mu C$

$V_{B}-\frac{q_{2}}{20}=V_{A}\Rightarrow V_{B}-V_{A}=+5 V$

$\Rightarrow$ (a) is correct.

For capacitor 1,

$q_{1}=200[1-e^{-\frac{t}{l}}]\mu C\Rightarrow i_{1}=\frac{1}{5}e^{-\frac{t}{l}}mA$

For capacitor 2,

$q_{2}=100[1-e^{-\frac{t}{l}}]\mu C\Rightarrow i_{2}=\frac{1}{10}e^{-\frac{t}{l}}mA$

$\Rightarrow V_{B}-\frac{q_{2}}{20}+i_{1}\times 25=V_{A}$

$\Rightarrow V_{B}-V_{A}=5[1-e^{-t}]-5e^{-t}$

     $=-5[1-2e^{-t}]$

 At t=ln 2,

  $V_{B}-V=5[1-1]=0$

$\Rightarrow$ (b) is correct.

At t=1,

 $i=i_{1}+i_{2}=\frac{1}{5}e^{-1}+\frac{1}{10}e^{-1}=\frac{3}{10}.\frac{1}{e}$

At t=0

$i=i_{1}+i_{2}=\frac{1}{5}+\frac{1}{10}=\frac{3}{10}$

$\Rightarrow$ (c) is correct

 After a long time , $i_{1}=i_{2}=0$

$\Rightarrow$ (d) is correct.