Discussion Forum



1)

A block with mass M is connected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0. Consider two cases : (i) when the block is at x0  and (ii) when the block is at x=x0 +A . In both the cases, a particle with mass m (<M)  is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?


A) The amplitude of oscillation in the first case changes by a factor of $\sqrt{\frac{M}{m+M}}$ whereas in the second case it remains unchanged

B) The final time period of oscillation in both the cases is same

C) The total energy decreases in both the cases

D) The instantaneous speed at $x_{0}$ of the combined masses decreases in both the cases.

Answer:

Option A,B,D

Explanation:

Case-1

1122021272_b12.JPG

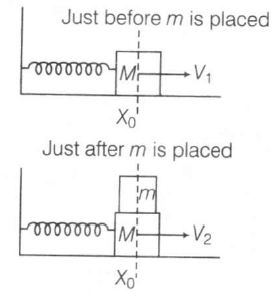
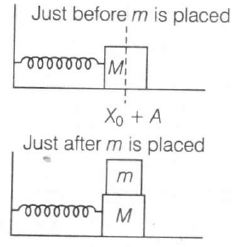
Case -II

1122021900_B13.JPG

In caes-I

$Mv_{1}=(M+m)v_{2}\Rightarrow v_{2}=(\frac{M}{M+m})v_{1}$

$\sqrt{\frac{k}{M+m}}A_{2}=(\frac{M}{M+m})\sqrt{\frac{k}{M}}A_{1}$

$A_{2}=\sqrt{\frac{k}{M+m}}A_{1}$

In case-2,     $A_{2}=A_{1}$

$T=2\pi \sqrt{\frac{M+m}{k}}$ in both cases.

 Total energy decreases in first case whereas remain same in 2nd case. Instantaneous speed at x0 decreases in both cases.