Answer:
Option C,D
Explanation:
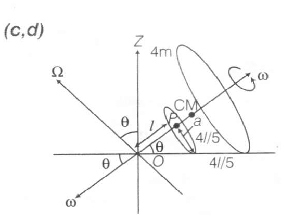
cosθ=1√l2+a2=√245
(c) Velcocity of point P:aω=1Ω then
Ω = aω1= Angular velocity of C M w.r.t
Point O. Angular velocity fo CM w.r.t Z - axis = Ω cosθ
ωCM−Z=aω1√245=aω√24a√245
ωCM−Z=aω5
(a) Lz=LCM−0cosθ−LD−CMsinθ
=81√245a2mω×√245−17ma2ω2×1√24
=81×24ma2ω25−17ma2ω2√24
(b) LCM−O=(5m)[9l5Ω]9l5=81ml2ω5
=81ml25×aωl
LCM−O=81mlaω5=81√24a2mω5
(d) LD−CM=ma22ω+4m(2a)22ω=17ma2ω2