Discussion Forum

A small object is placed 50cm to the left of a thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle θ=30°  to the axis of the lens, as shown in figure

 If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x,y) at which the image is formed are

Answer:

Explanation:

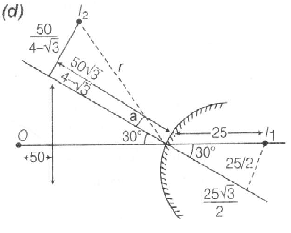
For Lens

$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\Rightarrow v=\frac{uf}{u+f}$

$v=\frac{(-50)(30)}{-50+30}=75cm$

For Mirror

   $\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\Rightarrow v=\frac{u f}{u-f}$

$\Rightarrow v=\frac{(\frac{25\sqrt{3}}{2})(50)}{\frac{25\sqrt{3}}{2}-50}=\frac{-50\sqrt{3}}{4-\sqrt{3}}cm$

$m=-\frac{v}{u}=\frac{h_{2}}{h_{1}}$

$\Rightarrow h_{2}=-[\frac{\frac{-50\sqrt{3}}{4-\sqrt{3}}}{\frac{25\sqrt{3}}{2}}]\frac{25}{2}\Rightarrow h_{2}=\frac{+50}{4-\sqrt{3}}$

The x-coordinate of the images

$=50-v \cos 30+h_{2} \cos 60 \approx 25$

The v-coordinate of the images

$=v\sin 30+h_{2}\sin60 \approx 25\sqrt{3}$