Discussion Forum

The ends Q and R of two thin wires, PQ and RS, are soldered (joined) together. Initially, each of the wire has a length of 1m 10⁰ C. Now, the end P is maintained at 10° C, While the end S is heated and maintained at 400° C. The system is thermally insulated from its surroundings. If the thermal conductivity of wire PQ is twice that of the wire RS and the coefficient of linear thermal expansion of PQ is  $1.2 \times 10^{-5}K^{-1}$, the change in length of the wire PQ is

Answer:

Explanation:

Rate of heat flow from P to Q,

$\frac{\text{d}Q}{\text{d}t}= \frac{2KA(T-10)}{1}$

 Rate of heat flow from Q to S

$\frac{\text{d}Q}{\text{d}t}= \frac{KA(4000-T)}{1}$

At steady state, state rate of heat flow is same

$\therefore \frac{2KA(T-10)}{1}= KA(400-T)$

or  2T-20=400-T  or 3T=420

    T= 140°

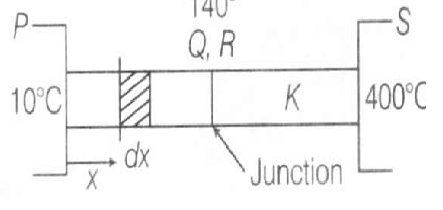
The temperature of the junction is 140° C.

Temperature at  a distance x from end P is T_x = (130 x+10°)

 Change in lenght dx is suppose dy

Then,  $dy=\propto dx(T_{x}-10)$

$\int_{0}^{\triangle y} dy= \int_{0}^{1} \propto dx(130x+10-10)$

$\triangle y=[\frac{\alpha x^{2}}{2}\times130]_0^1$

$\triangle y=1.2\times 10^{-5}\times 65$

$\triangle y= 78 \times 10^{-5}m=0.78 m$