Discussion Forum



1)

A transparent slab of thickness d has a refractive index n (z)that increases with z. Here, z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2 (> n2 ) as shown in the figure. A ray of light is incident with angle θi , from medium 1 and emerges in medium 2 with refraction angle θf with a lateral displacement l.

61202121_10a.JPG

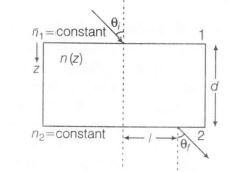
Which of the following statement(s) is (are) true


A) l is independent on n(z)

B) $n_{1} \sin \theta_{i}=(n_{2}-n_{1})\sin \theta_{f} $

C) $n_{1} \sin \theta_{i}=n_{2} \sin \theta_{f}$

D) l is independent of $n_{2}$

Answer:

Option A,C,D

Explanation:

From Snell's law,

$n \sin \theta= constant$

$n_{1} \sin \theta_{i}= n_{2} \sin \theta_{f} $

Further, I will depend on n1 and n(z). But it will be independent of n2