Discussion Forum



1)

A conducting loop in the shape of a right-angled isosceles triangle of height 10 cm is kept such that the 900 vertex is very close to an infinitely long conducting wire (see the figure). The wire is electrically insulated from the loop. The hypotenuse of the triangle is parallel to the wire. The current in the triangular loop is in the counterclockwise direction and increased at a constant rate of 1OAs-1  which of the following statement is (are) true?

512021285_7a.JPG


A) There is a repulsive force between the wire and the loop

B) If the loop is rotated at a constant angular speed about the wire, an additional emf of $\left(\frac{\mu_{0}}{\pi}\right)$ volt is induced in wire

C) The magnitude of induced emf in the wire $\left(\frac{\mu_{0}}{\pi}\right)$ volt

D) The induced current in the wire is in opposite direction to the current along the hypotenuse

Answer:

Option A,C

Explanation:

By reciprocity theorem of mutual induction, it can be assumed that current in the infinite wire is varying at l0A"/s and EMF is induced in the triangular loop.

512021139_7b.JPG

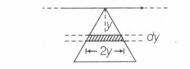
Flux of magnetic field through the triangle loop, if current in infinite wire is Q, can be calculated as follows:

 

$d\phi=\frac{\mu_{0}i}{2\pi y}.2ydy$

$d\phi=\frac{\mu_{0}i}{\pi}dy\Rightarrow \phi=\frac{\mu_{0}i}{\pi}\left(\frac{1}{\sqrt{2}}\right)$

$EMF=\mid \frac{\text{d}\phi}{\text{d}t}= \frac{\mu_{0}}{\pi}\left(\frac{1}{\sqrt{2}}\right).\frac{\text{d}i}{\text{dt}}$

$=\frac{\mu_{0}}{\pi}(10cm)\left(10\frac{A}{s}\right)=\frac{\mu_{0}}{\pi}$ volt

If we assume the current in the wire towards right then as the flux in the loop increases we know that the induced current in the wire is counter clockwise. Hence, the current in the wire is towards right. Field due to triangular loop at the location of infinite wire is into the paper. Hence, the force on the infinite wire is away from the loop. By cylindrical symmetry about infinite wire, rotation of triangular loop will not cause any additional EMF.