Discussion Forum

A plano-convex lens is made of material of refractive index n. When a small object is placed 30 cm away in front of the curved surface of the lens, an image of double the size of the object is produced. Due to reflection from the convex surface of the lens, another faint image is observed at a distance of 10 cm away from the lens. Which of the following statement(s) is (are) true?

Answer:

Explanation:

Case 1

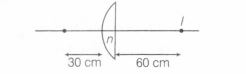
Using lens formula

$\frac{1}{60}+\frac{1}{30}=\frac{1}{f}$

$\Rightarrow \frac{1}{f}=\frac{1}{60}+\frac{2}{60}$

$\Rightarrow f=20 cm $

Further $\frac{1}{f_{1}}=(n-1)\left(\frac{1}{R}-\frac{1}{\infty}\right)$

$f_{1}=\frac{R}{n-1}=+20 cm $

Case 2

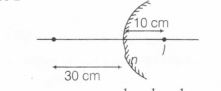
Using mirror formula

$\frac{1}{10}-\frac{1}{30}=\frac{1}{f_{2}}$

$\frac{3}{30}-\frac{1}{30}=\frac{1}{f_{2}}=\frac{2}{30}$

$f_{2}=15=\frac{R}{2} \Rightarrow R=30$

$\frac{R}{n-1}=+20 cm = \frac{30}{n-1}$

$\Rightarrow 2n-2 = 3$

$\Rightarrow f_{1}=+20 cm$

Refractive index of lens is 2.5. Radius of curvature of convex surface is 30 cm. Faint image is erect and virtual. Focal length of lens is 20 cm .