Discussion Forum



1)

 If the angles of elevation of the top of a tower from three  collinear points A, B and C on a line leading  to the foot of the tower are 30° , 45° and 60° respectively , then the ratio AB:BC is


A) $\sqrt{3}:1$

B) $\sqrt{3}:\sqrt{2}$

C) $1:\sqrt{3}$

D) 2:3

Answer:

Option A

Explanation:

 According to the given information.

the figure should be as follows.

  Let the height of tower =h

432021637_mm.JPG

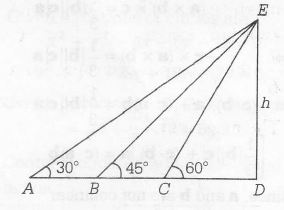
 In   $\triangle EDA$,

    $\tan 30^{0}=\frac{ED}{AD}$

  $\frac{1}{\sqrt{3}}=\frac{ED}{AD}=\frac{h}{AD}$

$\Rightarrow$                    $AD =h\sqrt{3}$

 In  $\triangle EDB$,

                        $\tan 45^{0}=\frac{h}{BD}\Rightarrow BD=h$

 $\triangle EDC$

                 $\tan 60^{0}=\frac{h}{CD}\Rightarrow CD=\frac{h}{\sqrt{3}}$

 Now,        $\frac{AB}{BC}=\frac{AD-BD}{BD-CD}$

 $\Rightarrow$       $\frac{AB}{BC}=\frac{h\sqrt{3}-h}{h-\frac{h}{\sqrt{3}}}$

$\Rightarrow$         $\frac{AB}{BC}=\frac{h(\sqrt{3}-1)}{\frac{h(\sqrt{3}-1)}{\sqrt{3}}}$

 $\Rightarrow$                 $\frac{AB}{BC}=\frac{(\sqrt{3}-1)}{(\sqrt{3}-1)}\times \sqrt{3}$

 $\Rightarrow$                 $\frac{AB}{BC}=\frac{\sqrt{3}}{1}$

$\therefore$    AB:BC=   $\sqrt{3}:1$