Discussion Forum

 Let O be the vertex and Q be any point on the parabola   $x^{2}=8y$. If the point P divides the line segment OQ internally in the ratio 1:3, then the locus of P is

Answer:

Explanation:

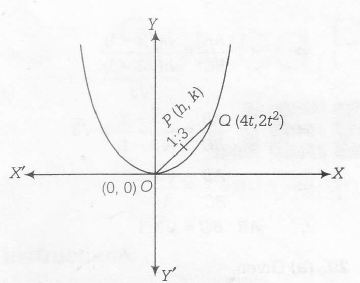
 Central Idea.    Any point on the parabola   $x^{2}=8y$   is (4t,2t²) Point P divides the line segment joining of O(0,0) and

Q (4t,2t² ) in the ratio 1:3, Apply the section formula for internal division.

 Equation of parabola is   $x^{2}=8y$           .............(i)

 Ler any point  Q on the parabola (i) is   (4t, 2t²  )

 Let P (h,k)  be the point which divides the line segment joining (0,0) and ( 4t, 2t²)  in the ratio 1;3

$\therefore$   $h=\frac{1\times4t+3\times0}{4}$

$\Rightarrow$      $h=t$

 and    $k=\frac{1\times 2t^{2}+3\times 0}{4d}$

  $\Rightarrow$         $k=\frac{t^{2}}{2}$

  $\Rightarrow$     $k=\frac{1}{2}h^{2}$

   $\Rightarrow$   2k=h²   $\Rightarrow$ 2y=  $x^{2}$, which is required locus