Answer:
Option D
Explanation:
Given equation of ellipse is
$\frac{x^{2}}{5}+\frac{y^{2}}{5}=1$
$\therefore$ $a^{2}=9,b^{2}=5$
$\Rightarrow$ a=3, $b=\sqrt{5}$
Now, $e=\sqrt{1-\frac{b^{2}}{a^{2}}}=\sqrt{1-\frac{5}{9}}=\frac{2}{3}$
foci $= (\pm ae, 0)= (\pm 2,0)$ and $\frac{b^{2}}{a}=\frac{5}{3}$
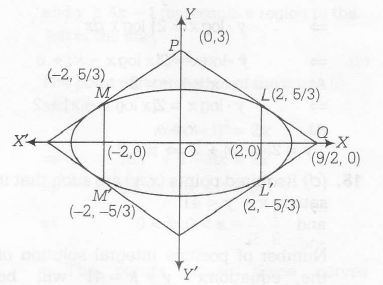
$\therefore$ Extremities of one latusrectum are
$(2,\frac{5}{3})$
$(2,\frac{-5}{3})$
$\therefore$ Equation of tangent at $(2,\frac{5}{3})$ is
$\frac{x(2)}{9}+\frac{y(5/3)}{5}=1$
or 2x+3y= 9.......(ii)
Eq .(ii) intersects X and Y axes at $(\frac{9}{2},0)$
and (0,3) , respectively
$\therefore$ Area of quadrilateral
= $4\times $ Area of $\triangle POQ $
= $4\times \left(\frac{1}{2} \times \frac{9}{2}\times 3\right)=27 sq.unit$
