Discussion Forum

The number of points having both coordinates as integers that lie in the interior of the triangle with vertices (0,0),(0,41) and (41,0). is

Answer:

Explanation:

Required points (x,y) are such that is satisfy  x+y <41

   and    x>0,y>0

   Number of positive integral solution of the  equation x+y+k=41 will be number of integral coordinates in the bounded region.

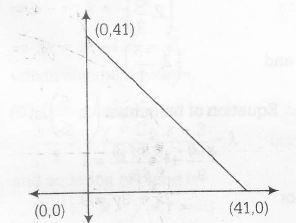
  $\therefore$   Total number of integral  coordinates

        $=^{41-1}C_{3-1}=^{40}C_{2}=\frac{40!}{2!38!}=780$

  Alter

 Consider the following figure.

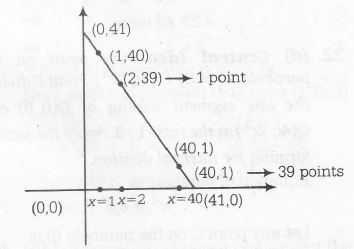
Clearly, the number of requires points

            = 1+2+3+.......+39

    $=\frac{39}{2}(39+1)=780$