Answer:
Option D
Explanation:
Given region is $(x,y:y^{2}\leq2x)$ and $(y\geq4x-1)$
$y^{2}\leq 2x$ represents a region inside the parabola
$y^{2}= 2x$ ..............(i)
and $y\geq 4x-1$ represents a region to the left of the line
y=4x-1 .......(ii)
The point of intersection of the curve (i) and (ii) is
$( 4x-1)^{2}=2x$
$\Rightarrow$ $16x^{2}+1-8x=2x$
$\Rightarrow$ $16x^{2}-10x+1=0$
$\Rightarrow$ $x=\frac{1}{2},\frac{1}{8}$
$\therefore$ The points where these curves interset , are $\left(\frac{1}{2},1\right)$ and $\left(\frac{1}{8},\frac{1}{2}\right)$
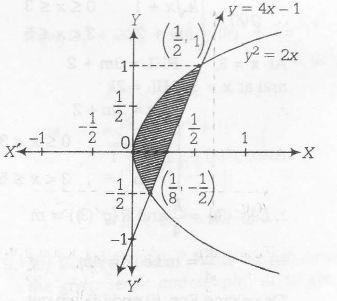
Hence, required area
= $\int_{-1/2}^{1} \left( \frac{y+1}{4}-\frac{y^{2}}{2}\right)dy$
= $\frac{1}{4}\left(\frac{y^{2}}{2}+y\right)_{-1/2}^1-\frac{1}{6}(y^{3})^{1}_{-1/2}$
= $\frac{1}{4}\left\{\left(\frac{1}{2}+1\right)-\left(\frac{1}{8}-\frac{1}{2}\right)\right\}-\frac{1}{6}\left\{1+\frac{1}{8}\right\}$
= $\frac{1}{4}\left\{\frac{3}{2}+\frac{3}{8}\right\}-\frac{1}{6}\left\{\frac{9}{8}\right\}$
= $\frac{1}{4}\times \frac{15}{8}-\frac{3}{16}=\frac{9}{32}$
