Discussion Forum



1)

Two long current carrying thin wires, both with current I, are held by insulating threads of length L and are in equilibrium as shown in the figure, with threads making an angle θ with the vertical. If wires have mass λ per unit length then, the value of I  is (g= gravitational acceleration)

2622021932_m29.JPG


A) $\sin\theta\sqrt{\frac{\pi \lambda gL}{\mu_{0}\cos\theta}}$

B) $2\sin\theta\sqrt{\frac{\pi \lambda gL}{\mu_{0}\cos\theta}}$

C) $2\sqrt{\frac{\pi g L}{\mu_{0}}\tan\theta}$

D) $\sqrt{\frac{\pi \lambda g L}{\mu_{0}}\tan\theta}$

Answer:

Option B

Explanation:

Consider free body diagram of the wire.

 As the wires are in equilibrium, they must carry current in the opposite direction

2622021209_m33.JPG

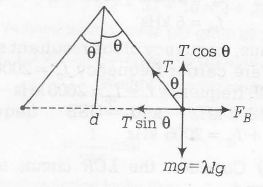
 Here,  $F_{B}=\frac{\mu_{0}I^{2}l}{2\pi d}$, where l is length of each wire and d is separation between wires.

 From figure,   $d=2L \sin\theta$

                $T=\cos\theta=mg=\lambda lg$ (in vertical direction) ......(i)

                      $T \sin\theta=F_{B}=\frac{\mu_{0}I^{2}l}{4\pi L\sin\theta}$

                                         ( in horizontal direction 0   .....(ii)

From Eqs. (i) and (ii)

  $\frac{T \sin\theta}{T\cos\theta}=\frac{\mu_{0}I^{2}l}{4\pi L\sin\theta\times\lambda lg}$

  $\therefore$              $I= \sqrt{\frac{4\pi\lambda L g \sin^{2}\theta}{\mu_{0}\cos\theta}}$

                    $=2\sin\theta \sqrt{\frac{\pi\lambda Lg}{\mu_{0}\cos\theta}}$