Discussion Forum

1)

From a solid sphere of mass M and radius R, a spherical  portion of radius  $\left(\frac{R}{2}\right)$   is  removed as shown in the figure. Taking gravitational potential V=0 at r= ∞ , the potential at the centre  of the cavity thus formed is (G= gravitational  constant)

Answer:

Option B

Explanation:

Central Idea      Consider cavity as negative mass and apply superposition of gravitatiional potential.

       Consider , the cavity formed in a solid sphere as shown in figure

                        V(∞)=0

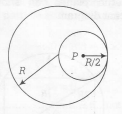
According to the question, we can write potential at an internal point P due to the complete solid sphere.

     $V_{s}=-\frac{GM}{2R^{3}}\left[3R^{2}-\left(\frac{R}{2}\right)^{2}\right]$

      $=-\frac{GM}{2R^{3}}\left[3R^{2}-\frac{R^{2}}{4}^{}\right]$

    $=-\frac{GM}{2R^{3}}\left[\frac{11R^{2}}{4}^{}\right]=\frac{-11GM}{8R}$

 Mass of removed part

    $=\frac{M}{\frac{4}{3}\times\pi R^{3}}\times\frac{4}{3}\times\pi\left(\frac{R}{2}\right)^{3}=\frac{M}{8}$

  Potential at  point P due to removed part

  $V_{c}=\frac{-3}{2}\times\frac{GM/8}{\frac{R}{2}}=\frac{-3GM}{8R}$

Thus, potential due to remaining part at point P.

      $V_{p}=V_{s}-V_{c}=\frac{-11GM}{8R}-\left(-\frac{3GM}{8R}\right)$

   $=\frac{(-11+3)GM}{8R}=\frac{-GM}{R}$