Answer:
Option C
Explanation:
Central idea:
Use geometry of the figure to calculate mass and side length of the cube interns of M and R respectively.
Consider the cross-sectional view of a diametric plane as shown in the adjacent diagram.
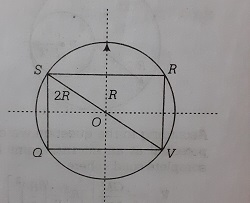
Cross-sectional view of the cube and sphere
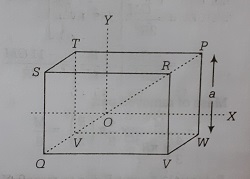
Using geometry of the cube
$PQ=2R=(\sqrt{3}a)$ or $a=\frac{2R}{\sqrt{3}}$
Volume density of the solid sphere
$\rho=\frac{M}{\frac{4}{3}\pi R^{3}}=\frac{3}{4\pi}\left(\frac{M}{R^{3}}\right)$
Mass of cube $(m)=(\rho)(a)^{3}$
$=\left(\frac{3}{4\pi}\times \frac{M}{R^{3}}\right)$
$=\left(\frac{3}{4\pi}\times \frac{M}{R^{3}}\right)\left[\frac{2R}{\sqrt{3}}\right]^{3}$
$=\frac{3M}{4\pi R^{3}}\times \frac{8R^{3}}{3\sqrt{3}}$
$\frac{2M}{\sqrt{3}\pi}$
Moment of interia of the cube about given axis is
$=\frac{3M}{4\pi R^{3}}\times \frac{8R^{3}}{3\sqrt{3}}$
$I_{y}\frac{ma^{2}}{6}=\frac{2M}{\sqrt{3}\pi}\times \frac{1}{6}\times \frac{4R^{2}}{3}=\frac{4MR^{2}}{9\sqrt{3}\pi}$