Discussion Forum

A particle of mass m moving in the x-direction with speed 2v is hit by another particle of mass 2m moving in the y-direction with speed v .If the collosion is perfectly inelastic the percentage loss in the eneergy during the collosion is close to

Answer:

Explanation:

Central Idea: Conservation of linear momentum can be applied but energy is not conserved.Consider the movement of two particles as shown below.

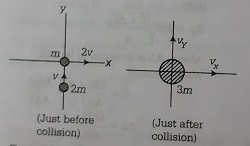
Conserving linear momentum in x-direction 

(p_i)x=(p_f)x

or 2mv=(2m+m)v_x

v_x=$\frac{2}{3}v$

Considering linear momentum in y-direction

(p_i)y=(p_f)y

or 2mv=(2m+m)vy

V_y=$\frac{2}{3}v$

Initial kinetic energy of two particles sysytem is 

$E_{i}=\frac{1}{2}m(2v^{2})+\frac{1}{2}(2m)(v)^{2}$

$=\frac{1}{2}4mv^{2}+\frac{1}{2}2mv^{2}$

$3mv^{2}$

Final energy of the combined two particles system is 

$E_{f}=\frac{1}{2}(3m)(v_x^2+v_y^2)$

$=\frac{1}{2}(3m)\left[\frac{4v^{2}}{9}+\frac{4v^{2}}{9}\right]$

$=\frac{3m}{2}\left[\frac{8v^{2}}{9}\right]=\frac{4mv^{2}}{3}$

loss in the energy 

$\Delta E=E_{i}-E_{f}$

$mv^{2}\left[3-\frac{4}{3}\right]=\frac{5}{3}mv^{2}$

Percentage loss in the energy during the collision

$\frac{\Delta E}{Ei}\times 100=\frac{\frac{5}{3}mv^{2}}{3mv^{2}}\times 100=\frac{5}{9}\times 100$

$\simeq 56%$