Discussion Forum



1)

Let n1  and n2  be the number of red and black balls. respectively in box I. Let  n3 and n4  be the number of red and black balls respectively in box II.

A ball is drawn at random from box  I and transferred to box II. If the probability  of drawing  a red ball from box I, after this transfer  is  $\frac{1}{3}$, then the correct option(s)  with the possible values of n1 and n2  is/are


A) $n_{1}=4$ and $n_{2}=6$

B) $n_{1}=2$ and $n_{2}=3$

C) $n_{1}=10$ and $n_{2}=20$

D) $n_{1}=3$ and $n_{2}=6$

Answer:

Option C,D

Explanation:

1432021167_m3.JPG

1432021836_m4.JPG

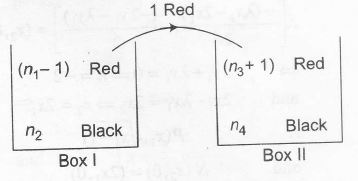
$\therefore$     P (drawing  red ball from B1)=  $\frac{1}{3}$

  $\Rightarrow$                     $\left(\frac{n_{1}-1}{n_{1}+n_{2}-1}\right)\left(\frac{n_{1}}{n_{1}+n_{2}}\right)+\left(\frac{n_{2}}{n_{1}+n_{2}}\right)\left(\frac{n_{1}}{n_{1}+n_{2}-1}\right)=\frac{1}{3}$

$\Rightarrow$         $\frac{n_1^2+n_{1}.n_{2}-n_{1}}{(n_{1}+n_{2})(n_{1}+n_{2}-1)}=\frac{1}{3}$

   Clearly, options  (c) and (d)  satisfy