Discussion Forum



1)

In a thin rectangular metallic strip a constant current I flows along the positive x-direction, as shown in the figure. The length,  width and thickness of the strip are l, w and d respectively. A uniform magnetic field  B is applied on the strip along the positive y-direction. Due to this, the charge carriers experience a net deflection along the z-direction. This results in the accumulation of charge carries on the surface PQRS and appearance of equal and opposite charges on the face opposite to PQRS. A potential difference along the z-direction is thus developed. Charge accumulation continues untill the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross-section  of the strip and carried by electrons.

1032021606_p2.JPG

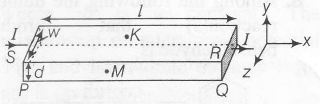
Consider two different metallic strips (1 and 2 )  of the same material. Their lengths are the same , width  are w1   and w2  and thickness  are d1 and d2 , respectively. Two points K and M are symmetrically  located on the opposite  faces parallel to the x-y plane  (see figure) .V1 and V2  are the potential  differences  between K and M in strips 1 and 2 respectively. Then , for  a given  current I flowing through  them in a given  magnetic field  strength  B, the correct statements is/are


A) if $w_{1}=w_{2}$ and $d_{1}=2d_{2}$, then $V_{2}=2V_{1}$

B) If $w_{1}=w_{2}$ and $d_{1}=2d_{2}$, then $V_{2}=V_{1}$

C) If $w_{1}=2w_{2}$ and $d_{1}=d_{2}$, then $V_{2}=2V_{1}$

D) If $w_{1}=2w_{2}$ and $d_{1}=d_{2}$, then $V_{2}=V_{1}$

Answer:

Option A,D

Explanation:

$ F_{B}=B_{ev}=B_{e}\frac{1}{nAe}=\frac{BI}{nA}$

     Fe= eE

   $\Rightarrow$           Fe    =FB

                               $eE=\frac{BI}{nA}$

  $\Rightarrow$                $E=\frac{B}{nAe}$

                                     $V=Ed=\frac{BI}{nAe}.w=\frac{BIw}{n(wd)e}=\frac{BI}{ned}$

                                        $\frac{V_{1}}{V_{2}}=\frac{d_{2}}{d_{1}}$

  $\Rightarrow$                        $E=\frac{B}{nAe}$

                              $V=Ed=\frac{BI}{nAe}.w=\frac{BIw}{n(wd)e}=\frac{BI}{ned}$

                          $\frac{V_{1}}{V_{2}}=\frac{d_{2}}{d_{1}}$

    $\Rightarrow$  if w1    =2w2   and d1  =d2

                                                  V1  =V2

$\therefore$   Correct answes are (a) and (d)