Discussion Forum

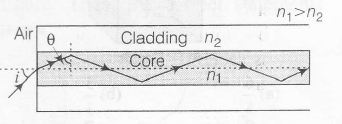
Light guidance in an optical fibre can be understood by considering a structure comprising of thin solid glass cylinder of refractive index n₁  surrounded by a medium of lower refractive index n₂. The light guidance in the structure takes place due to successive total internal reflections at the interface of the media n₁  and n₂ as shown in the figure. All rays with the angle of incidence i less than a particular value i_m are confined in the medium of refractive index n₁. The numerical aperture  (NA) of the structure is defined as sin I'm.

For two structures namely S₁   with $n_{1}=\frac{\sqrt{45}}{4}$  and   $n_{2}=\frac{3}{2}$   and S₂    with $n_{1}=\frac{8}{5}$  and $n_{2}=\frac{7}{5}$  and taking the  refractive index of water to be $\frac{4}{3}$  and that to air to be 1. the correct options is/are

Answer:

Explanation:

  $\frac{4}{3}\sin i=\frac{\sqrt{45}}{4}\sin(90-\theta_{c})=\frac{\sqrt{45}}{4}\cos \theta_{c}$

                                       $\sin \theta_{c}=\frac{n_{2}}{n_{1}}$

  $\therefore$                    $\cos \theta_{c}=\sqrt{1-\left(\frac{n_{2}}{n_{1}}\right)^{2}}$

            $\Rightarrow$                   $\frac{4}{3} \sin i=\frac{\sqrt{45}}{4}\frac{3}{\sqrt{45}}$

                                               $\sin i=\frac{9}{16}$

 In second case,

                          $\sin \theta_{c}=\frac{n_{2}}{n_{1}}=\frac{7}{8}$

 $\Rightarrow$                  $\cos \theta_{c}=\frac{\sqrt{15}}{8}$   

                      $\frac{16}{3\sqrt{15}}\sin i=\frac{5}{8}\sin (90-\theta)$

 Simplifying we get,   $\sin i=\frac{9}{16}$

  (a) is correct.

 Same approach can be adopted for other options. Correct answers are (a)  and (c).