Discussion Forum

An ideal monoatomic gas is confined ina horizontal cylinder by a spring-loaded piston  (as shown in the figure). Initially, the gas is at temperature T₁,  pressure P₁  and volume V₁  and the spring is in its relaxed state.  The gas is then heated very slowly to temperature T₂, pressure P₂  and volume V₂  . during this process the piston moves out  by a distance of x, Ignoring the friction  between the piston and the cylinder, the correct statements is/are

Answer:

Explanation:

 Note:   This question can be solved if the right-hand side chamber is assumed to open so that its pressure remains constant even if the piston shifts towards night.

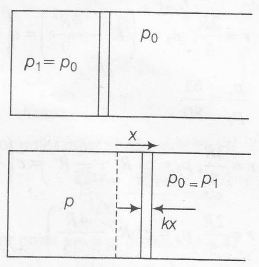
(a)    $pV=n RT \Rightarrow p \propto\frac{T}{V}$

 Temperature  is  made three times and volume is doubled

$\Rightarrow$       $p_{2}=\frac{3}{2}p_{1}$

     Further        $x=\frac{\triangle V}{A}=\frac{V_{2}-V_{1}}{A}$

                                  $=\frac{2V_{1}-V_{1}}{A}=\frac{V_{1}}{A}$

                     $p_{2}=\frac{3p_{1}}{2}=p_{1}+\frac{kx}{A}$

$\Rightarrow$     $KX=\frac{P_{1}A}{2}$

    Energy of spring

              $\frac{1}{2}kx^{2}=\frac{p_{1}A}{4}x=\frac{p_{1}V_{1}}{4}$

(b)       $\triangle U=nc_{v}\triangle T=n\left( \frac{3}{2}R\right) \triangle T$

                           = $\frac{3}{2}(p_{2}V_{2}-p_{1}V_{1})$

                    $\frac{3}{2}\left[ \left(\frac{3}{2}P_{1}\right) (2V_{1})-p_{1}V_{1}\right]=3p_{1}V_{1}$

  (c)                        $p_{2}=\frac{4p_{1}}{3}\Rightarrow p_{2}=\frac{4}{3}p_{1}=p_{1}+\frac{kx}{A}$

            $\Rightarrow$           $kx=\frac{p_{1}A}{3}\Rightarrow x=\frac{\triangle V}{A}=\frac{2V_{1}}{A}$

                                     $W_{gas}=(p_{0}\triangle V +W_{spring})$

                  $=(p_{1}Ax+\frac{1}{2}kx.x)$

$=+\left( p_{1}A.\frac{2V_{1}}{A}+\frac{1}{2}.\frac{p_{1}A}{3}.\frac{2V_{1}}{A}\right)$

                                  $=2p_{1}V_{1}+\frac{p_{1}V_{1}}{3}=\frac{7p_{1}V_{1}}{3}$

(d)

                 $\triangle Q=W+\triangle U$

  =      $\frac{7p_{1}V_{1}}{3}+\frac{3}{2}\left( p_{2}V_{2}-p_{1}V_{1}\right)$

           =   $\frac{7p_{1}V_{1}}{3}+\frac{3}{2}\left(\frac{4}{3}p_{1}.3V_{1}-p_{1}V_{1} \right)$

               =  $\frac{7p_{1}V_{1}}{3}+\frac{9}{2}p_{1}V_{1} =\frac{41p_{1}V_{1}}{6}$

 Note:  $\triangle U=\frac{3}{2}(p_{2}V_{2}-p_{1}V_{1})$   , has been obtained in part (b).