Discussion Forum

 A spherical  body of radius R consists  of a fluid  of constant density and is in equilibrium  under  its own gravity . If  P(r)  is the pressure  at r(r<R) , then  the correct options  is /are

Answer:

Explanation:

 Gravitational  field at a distance  r due to mass 'm'

        $E=\frac{G\rho \frac{4}{3}\pi r^{3}}{r^{2}}=\frac{4G\rho \pi r}{3}$

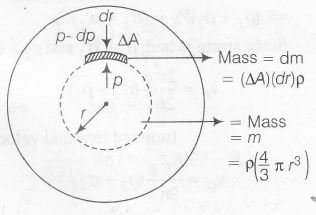
 Consider a small element  of width  dr and are  $\triangle A$    at a distance r.

  Pressure force on this element  outwards = gravitational force on 'dm'  from 'm'  inwards

        $\Rightarrow$          $(dp)\triangle A=E(dm)$

  $\Rightarrow$    $-dp.\triangle A=\left\{\frac{4}{3}G \pi \rho r\right\}(\triangle A.dr.\rho)$

$-\int_{0}^{P}dp=\int_{R}^{r}\left(\frac{4G\rho^{2}\pi}{3}  \right)rdr$

   $-p=\frac{4G\rho^{2}\pi}{3\times 2}[r^{2}-R^{2}]$

$\Rightarrow$     $P=c(R^{2}-r^{2})$

$r=\frac{3R}{4},p_{1}=c\left(R^{2}-\frac{9R^{2}}{16}\right)=c\left(\frac{7R^{2}}{16}\right)$

  $r=\frac{2R}{4},p_{2}=c\left(R^{2}-\frac{4R^{2}}{9}\right)=c\left(\frac{5R^{2}}{9}\right)$

    $\frac{p_{1}}{p_{2}}=\frac{63}{80}$

    $r=\frac{3R}{5},p_{3}=c\left(R^{2}-\frac{9}{25}R^{2}\right)=c\left(\frac{16R^{2}}{25}\right)$

  $r=\frac{2R}{5},p_{4}=c\left(R^{2}-\frac{4R^{2}}{25}\right)$

      $=c\left(\frac{21R^{2}}{25}\right)\Rightarrow\frac{p_{3}}{p_{4}}=\frac{16}{21}$