Discussion Forum

1)

A monochromatic beam of light is incident at 60° on one face of an equilateral prism of refractive index n  and emerges from the opposite face making an angle θ  (n) with the normal (see figure). For n=$\sqrt{3}$ the value of θ is 60° and $\frac{d\theta}{dn}=m,$   The value of m is 

Answer:

Option B

Explanation:

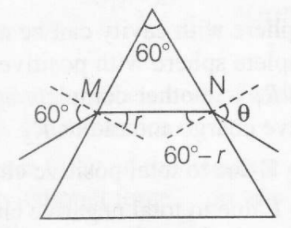
Appluing Snell's law at M and N,

  $\sin60^{0}=n\sin r$          ............(i)

    $\sin\theta=\pi\sin(60-r)$     ............(ii)

 Differentiating we get

         $\cos\theta\frac{d\theta}{dn}=-n\cos(60-r)\frac{dr}{dn}+\sin(60-r)$

 

Differentiating Eq.(i),

  $n\cos r\frac{dr}{dn}+\sin r=0$

or         $\frac{dr}{dn}=-\frac{\sin r}{n\cos r}=\frac{-\tan r}{n}$

   $\Rightarrow$               $\cos \theta \frac{d\theta}{dn}=-n\cos(60^{0}-r)\left[\frac{-\tan r}{n}\right]+\sin(60^{0}-r)$

                $\frac{d\theta}{dn}=\frac{1}{\cos\theta}\left[ \cos(60^{0}-r\right)\tan r+\sin(60^{0}-r)]$

  From Eq.(i)  , r =30°  for n=$\sqrt{3}$

                      $\frac{d\theta}{dn}=\frac{1}{\cos 60}(\cos 30\times \tan 30+\sin 30)$

                         $=2(\frac{1}{2}+\frac{1}{2})=2$