Discussion Forum

Let $\triangle PQR$  be a triangle . Let  a=QR, b= RP and  c= PQ . If  |a|=12, |b|= $4\sqrt{3}$ and  b.c=24, then which of the following is/are true?

Answer:

Explanation:

Given,  |a|= 12,   |b|= 4  $\sqrt{3}$

         a+b+c= 0

 $\Rightarrow$               a=-(b+c)

$\Rightarrow$        $|a|^{2}=|b+c|^{2}$

$\Rightarrow$                      $|a|^{2}=|b|^{2}+|c|^{2}+2 b.c$

$\Rightarrow$               $144=48+|c|^{2}+48$

$\Rightarrow$                   $|c|^{2}=48\Rightarrow |c|=4\sqrt{3}$

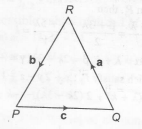
 Also,  $|c|^{2}=|a|^{2}+|b|^{2}+2.a.b$

$\Rightarrow$       48=144+48+2.a.b

$\Rightarrow$      a.b=-72

    $\therefore$  Option (d) is correct.

  Also,    a x b=c x a

$\Rightarrow$      a x b +c x a =2a x b

$\Rightarrow$          |a x b +c x a| =2|a x b|

                                                   =   $2\sqrt{|a|^{2}|b|^{2}-(a.b)^{2}}$

                  =   $2\sqrt{(144)(48)-(-72)^{2}}$

                =   $2(12)\sqrt{48-36}= 48\sqrt{3}$

. $\therefore$    Option (c) correct.

 Also,    $\frac{|c|^{2}}{2}-|a|=24-12=12$

$\therefore$    Option (a ) is  correct.

and 

            $\frac{|c|^{2}}{2}+|a|=24+12=36$

 $\therefore$    Option (b ) is  not   correct.