Discussion Forum

Let y(x) be a soilution of the differential equation $(1+e^{x})y^{'}+ye^{x}=1,$.If y(0)=2 , then which of the following statement(s) is/are true?

Answer:

Explanation:

Here , $(1+e^{x})y^{'}+ye^{x}=1,$

$\Rightarrow$                         $\frac{dy}{dx}+e^{x}.\frac{dy}{dx}+ye^{x}=1$

$\Rightarrow$                     $dy+e^{x}dy+ye^{x}dx=dx$

$\Rightarrow$                     $dy+d(e^{x}y) =dx$

  On integrating both sides, we get

                           $y+e^{x}y=x+C$

  Given      ,      y(0)=2

$\Rightarrow$      $2+e^{0}.2=0+C$

$\Rightarrow$      C=4

$\therefore$                       $y(1+e^{x})=x+4$

$\Rightarrow$                       $y=\frac{x+4}{1+e^{x}}$

  Now at x=-4,         $y=\frac{-4+4}{1+e^{-4}}=0$

  $\therefore$              y(-4)=0  ......(i)

  For  critical points,   $\frac{dy}{dx}=0$

i.e,   $\frac{dy}{dx}=\frac{(1+e^{x}).1-(x+4)e^{x}}{(1+e^{x})^{2}}=0$

$\Rightarrow$                      $e^{x}(x+3)-1=0$

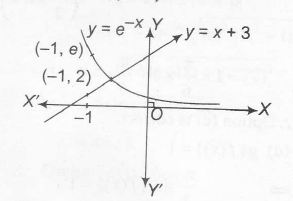
 or                       $e^{-x}=(x+3)$

  Clearly, the intersecting  point lies between (-1,0)

  $\therefore$     y(x) has a critical point in the interval (-1,0)