Discussion Forum

If the normals of the parabola  $y^{2}=4x$    drawn at the endpoints of the latus rectum  are tangents to the circle $(x-3)^{2}+(y+2)^{2}=r^{2}$, then the value of r² is 

Answer:

Explanation:

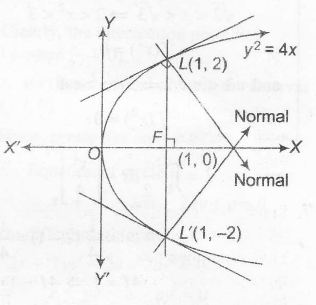
 End points of latusrectum are  $(a,\pm2a)$  i.e,  $(1,\pm2)$

 Equation  of normal at ( x₁, y₁) is   $\frac{y-y_{1}}{x-x_{1}}=-\frac{y_{1}}{2a}$

  i.e,                  $\frac{y-2}{x-1}=-\frac{2}{2}$

  and                $\frac{y+2}{x-1}=\frac{2}{2}$

  $\Rightarrow$             x+y=3

                and                 x-y=3

 which is tangent to 

           $(x-3)^{2}+(y+2)^{2}=r^{2}$

$\therefore$   Length of perpendicular from centre = Radius

 $\Rightarrow$   $\frac{|3-2-3|}{\sqrt{1^{2}+1^{2}}}=r$

   $r^{2}=2$