Discussion Forum

Let the curve C be the mirror image of the parabola  $y^{2}=4x$  with respect to the line  x+y+4=0, If A and B are the points  of intersection  of C with the line y=-5  , then the distance between A and B are

Answer:

Explanation:

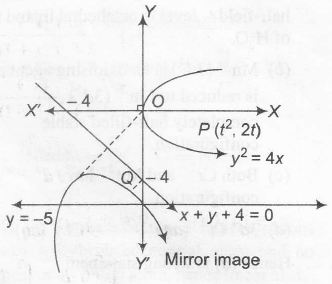
Let  P( t² ,2t)  be a point on the curve  $y^{2}=4x$ , whose image is Q(x,y)  on x+y+4=0, then

$\frac{x-t^{2}}{1}=\frac{y-2t}{1}$

$=\frac{-2(t^{2}+2t+4)}{1^{2}+1^{2}}$

$\Rightarrow$   x=-2t-4

   and            y$=-t ^{2}-4$

 Now, the straight line y=-5 meets the mirror image

  $\therefore$                  $-t ^{2}-4=-5$

  $\Rightarrow$     $t ^{2}=1$

$\Rightarrow$           $t=\pm1$

Thus, points of intersection of A and B are (-6,-5) and (-2,-5)

 $\therefore$ Distance , AB= $\sqrt{(-2+6)^{2}+(-5+5)^{2}}=4$