Discussion Forum

 A bullet is fired vertically upwards with velocity v from the surface of a spherical planet. When it reaches its maximum height, its acceleration due to the planet's gravity is  $\frac{1}{4}$th of its value at the surface of the planet. If the escape  velocity from the planet is  $v_{sec}=v\sqrt{N}$, then the value of N is  (ignore energy loss due to atmosphere)

Answer:

Explanation:

 At height h

                    $g'=\frac{g}{\left(1+\frac{h}{R}\right)^{2}}$      ......(i)

 Given, $g'=\frac{g}{4}$

 Substituting  in Eq .(i) we get,

                                    h=R

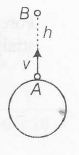
   Now, From A to B,

  Decrease in kinetic energy= increase in potential energy

$\Rightarrow$    $\frac{1}{2}mv^{2}=\frac{mgh}{1+\frac{h}{R}}$

$\Rightarrow$    $\frac{v^{2}}{2}=\frac{gh}{1+\frac{h}{R}}=\frac{1}{2}gR$              (h=R)

$\Rightarrow$    $v^{2}= gR$    or   $v= \sqrt{gR}$

  Now,      $v_{esc}=\sqrt{2gR}=v\sqrt{2}$

$\Rightarrow$                N=2