Discussion Forum

1)

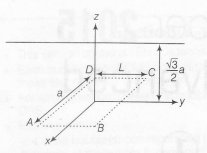
An infinitely long uniform line charge distribution of charge per unit length λ  lies parallel to the y-axis in the y-z plane at   

$z=\frac{\sqrt{3}}{2}a$    ( see figure). If the magnitude of the flux of the electric field through  the rectangular  surface ABCD lying in the x-y plane with its centre at the origin is   $\frac{\lambda L}{n \epsilon_{0}}$

                   ($\epsilon_{0}=$  = permittivity of free space) then the value of n is 

Answer:

Option D

Explanation:

 ANBP is cross-section of a cylinder of length L. The line charges pass through  the centre O and perpendicular to paper

$AM=\frac{a}{2},MO=\frac{\sqrt{3}a}{2}$

$\therefore$    $\angle AOM=\tan ^{-1}\left(\frac{AM}{OM}\right)$

                              $=\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=30^{0}$

 Electric Flux passing from the whole cylinder

                                                 $\phi_{1}=\frac{q_{in}}{\epsilon_{0}}=\frac{\lambda L}{\epsilon_{0}}$

  $\therefore$ Electric flux passing through ABCD plane surface  (shown only AB)= Electric flux  passing through cylindrical  surface ANB

                             =  $\left( \frac{60^{0}}{360^{0}}\right)(\phi_{1})=\frac{\lambda L}{6\epsilon_{0}}$

   $\therefore$              n=6