Discussion Forum

1)

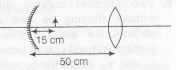
Consider a concave mirror and a  convex lens  ( refractive index=1.5) of focal length 10 cm each, separated by a distance of 50cm in air (refractive index=1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification M₁. When the set up is kept in a medium of refractive index. $\frac{7}{6}$, the magnification becomes M₂. The magnitude   $\mid\frac{M_{2}}{M_{1}}\mid$   is

Answer:

Option C

Explanation:

Case I

   Reflection from mirror

  $\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\Rightarrow\frac{1}{-10}=\frac{1}{v}+\frac{1}{-15}$

  $\Rightarrow$          v=-30

For lens              $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

                         $\frac{1}{10}=\frac{1}{v}-\frac{1}{-20}$

                                      v=20

     $|M_{1}|=|\frac{v_{1}}{u_{1}}||\frac{v_{2}}{u_{2}}|$

           $=\left(\frac{30}{15}\right)\left(\frac{20}{20}\right)$

    =  2 X 1=2        (in air)

Case  II For mirror , there is no change

 v=-30

For lens

$\frac{1}{f_{air}}=\left(\frac{3/2}{1}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$

      $\frac{1}{f_{medium}}=\left(\frac{3/2}{7/6}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$

 with            f_{air  =10cm}

 We get    $\frac{1}{f_{medium}}=\frac{4}{70}cm^{-1}$

              $\frac{1}{v}-\frac{1}{-20}=\frac{4}{70}$

$\frac{1}{v}+\frac{1}{20}=\left(\frac{2}{7}\right)\left(\frac{2}{10}\right)=\frac{4}{70}$

    $\frac{1}{v}=\frac{4}{70}-\frac{1}{20}$

    v=140,

     $|M_{2}|=|\frac{v_{1}}{u_{1}}||\frac{v_{2}}{u_{2}}|$

                             $=\left(\frac{30}{15}\right)\left(\frac{140}{20}\right)$

                           $=2\left(\frac{140}{20}\right)=14$

                        $\Rightarrow$      $|\frac{M_{2}}{M_{1}}|=\frac{14}{2}=7$