Discussion Forum



1)

A Young's double slit interference  arrangement with slits S1   and S2 is immersed in water (refractive index=4/3)  as shown in the figure. The positions pf maxima on the surface of water are given by   $x^{2}=p^{2}m^{2}\lambda^{2}-d^{2}$ , where  $\lambda$    is the wavelength  of light in air (refractive index=1)  , 2d is the seperation between the slits and m is an integer . The value of p is 

632021190_p1.PNG


A) 3

B) 4

C) 2

D) 1

Answer:

Option A

Explanation:

632021894_p2.PNG

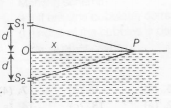
$\mu(S_{2}P)-S_{1}P=m\lambda$

$\Rightarrow$                $\mu\sqrt{d^{2}+x^{2}}-\sqrt{d^{2}+x^{2}}=m\lambda$

$\Rightarrow$              $(\mu-1)\sqrt{d^{2}+x^{2}}=m\lambda$

$\Rightarrow$             $(\frac{4}{3}-1)\sqrt{d^{2}+x^{2}}=m\lambda$

   or                      $\sqrt{d^{2}+x^{2}}=3m\lambda$

 Squaring this equation we get,

                $x^{2}=9m^{2}\lambda^{2}-d^{2}$

$\Rightarrow$       $P^{2}=9$          OR  P=3