Discussion Forum

 Let C be the circle with centre at (1,1) and radius 1. If T is the circle centred at (0,y)  passing through the origin and touching the circle C externally, then the radius of T is equal to 

Answer:

Explanation:

 Use the property, when two circles touch each other externally, then distance between the centre is equal to sum of their radii, to get the required radius.

 Let the coordinate of the centre of T be (0,k)

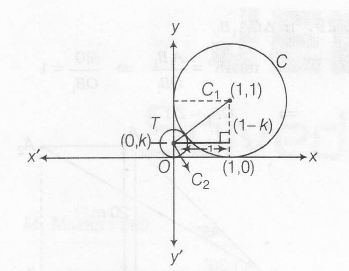
 Distance between their centre

   $k+1=\sqrt{1+(k-1)^{2}}  $           [  $\because $   C₁C2=k+1]

$\Rightarrow$      $ k+1= \sqrt{1+k^{2}+1-2k} $

$\Rightarrow$        $ k+1= \sqrt{k^{2}+2-2k} $

$\Rightarrow$        $ k^{2}+1+2k= k^{2}+2-2k $

$\Rightarrow$       k=1/4

So  , the radius of circle T is  k, i.e, 1/4