Discussion Forum

If PS  is the median of the triangle with vertices P(2,2), Q(6,-1). and R(7,3) then equation of the line passing through (1,-1) and parallel to PS is

Answer:

Explanation:

Coordinate of $S=\left(\frac{7+6}{2},\frac{3-1}{2}\right)$

= (13/2.1)

[  $\because$   S is mid-point of line QR]

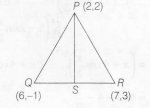
slop of the line   PS is   $\frac{-2}{9}$
Required equation passes through (1,-1) and parallel to PS is 

  $y+1=\frac{-2}{9}(x-1)$

  $\Rightarrow$    $2x+9y+7=0$