Discussion Forum

If  a ε R  and equation -3(x-[x])²+2(x-[x])+a²=0    (where,[x] denotes the greatest integer   $\leq$ x)  has no integral solution, then all possible values of  a lie  in the interval

Answer:

Explanation:

Put  t= x -[x]={X}, which  is a fractional part function and lie between    $0\leq \left\{x\right\}$  <1 and then solve it,

  Given    a ε R and equation is     

   -3(x-[x])²+2(x-[x])+a²=0   

  t=x-[x] , then equation is

$-3t^{2}+2t+a^{2}=0$

$\Rightarrow$      $t=\frac{1\pm\sqrt{1+3a^{2}}}{3}$

$\therefore$    t= x-[x]= {X}

                          { fractional part}

$\therefore$         $0\leq t\leq1$

                   $0\leq\frac{1\pm\sqrt{1+3a^{2}}}{3}\leq1$

Taking positive sign , we get 

     $0\leq\frac{1+\sqrt{1+3a^{2}}}{3}<1$                   [ $\therefore$ {x}>0}

$\Rightarrow$                $\sqrt{1+3a^{2}}<2\Rightarrow1+3a^{2}<4$

$\Rightarrow$                    a²-1<0

$\Rightarrow$            (a+1)(a-1)<0

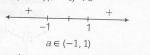
   for no integral  solution of a we consider the interval (-1,0) $\cup$  (0,1) .

Note.  here, we figure out the integral solution , we get a=0, This implies any interval excluding zero should be correct answer as it gives either  no solution or no integral.