Discussion Forum

If z is complex number such that   $|z|\geq 2$  then the minimum value of   $|z+\frac{1}{2}|$  

Answer:

Explanation:

$|z|\geq 2$  is the region on or outside circle whose centre is (0,0) and radius is 2 .

 Minimum   $|z+\frac{1}{2}|$   is distance of z, which

lie on circle |z|=2 from ( -$\frac{1}{2},0$)

   $\therefore$  Minimum  $|z+\frac{1}{2}|$ = Distance of ($-\frac{1}{2},0$) from (-2,0)

                       =$\sqrt{(-2+\frac{1}{2})^{2}+0}=\frac{3}{2}$

            = $\sqrt{(-\frac{1}{2}+2)^{2}+0}=\frac{3}{2}$

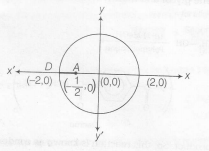
Geometrically min   $|z+\frac{1}{2}|$ = AD

Here minimum value of   $(z+\frac{1}{2}) $   lies in the intervel (1,2)