Discussion Forum



1)

CsCl crystallises in body centred cubic lattice. If a its edge length, then which of the following expression is correct?


A) $r_{cs^{-}}+r_{cl^{-}}=3a$

B) $r_{cs^{-}}+r_{cl^{-}}=\frac{3a}{2}$

C) $r_{Cs^{+}}+r_{Cl^{-}}=\frac{\sqrt{3}}{2}a$

D) $r_{Cs^{+}}+r_{Cl^{-}}=\sqrt{3}a$

Answer:

Option C

Explanation:

In CsCl,Cl- lie at  corners of simple cube and Cs+ at the body centre . Hence  , along the  body diagonal , Cs+ and Cl- touch each other so,

 $r_{Cs^{+}}+r_{Cl^{-}}=2r$

 Calculation of   $\tau$

In $\triangle EDF$

1632021673_P4.PNG

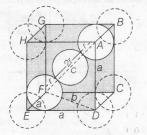
Body centred cubic unit cell

   $FD=b=\sqrt{a^{2}+a^{2}}=\sqrt{2}a$

  In  $\triangle AFD$, 

          $c^{2}=a^{2}+b^{2}$

               $=a^{2}+(\sqrt{2}a)^{2}$

   $=a^{2}+2a^{2}$

         $c^{2}=3a^{2}$

         $c=\sqrt{3}a$

As  $\triangle AFD$ is an equilateral triangle,

  $\therefore$     $\sqrt{3}a=4r$

  $\Rightarrow   r =\frac{\sqrt{3}a}{4}$

  Hence,   $r_{Cs^{+}}+r_{Cl^{-}}=2r$

                =  $2\times\frac{\sqrt{3}}{4}a=\frac{\sqrt{3}}{2}a$