Discussion Forum



1)

 Three rodes of copper, brass and steel are welded together to form a Y-shaped structure. Area of cross-section of each rod is 4 cm2. End of copper rod is maintained at 100° C whereas ends of brass and steel are kept at 0° C. Lengths of the copper, brass and steel rods are 46,13 and 12 cm respectively, The rods are thermally insulated from surroundings except at ends. Thermal conductivities are 0.92 ,0.26 and 0.12 in CGS units, respectively. Rate of heat flow through copper rod is 


A) 1.2 cal/s

B) 2.4 cal/s

C) 4.8 cal/s

D) 6.0 cal/s

Answer:

Option C

Explanation:

 In thermal conduction , it is found that in  steady state the heat current is direcly proportional to the area  of cross-section A which is proportional to the change in  temperature (T1-T2)

 Then,    $\frac{\triangle Q}{\triangle t}=\frac{KA(T_{1}-T_{2})}{x}$

  According to thermal conductivity , we get

1532021367_m13.JPG

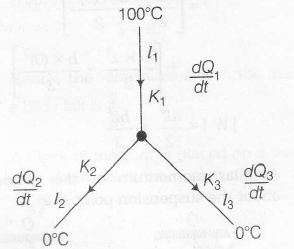
i.e,    $\frac{dQ_{1}}{dt}=\frac{dQ_{2}}{dt}+\frac{dQ_{3}}{dt}$

$\frac{0.92(100-T)}{46}=\frac{0.26(T-0)}{13}+\frac{0.12(T-0)}{12}$

$\Rightarrow $       $T=40^{0}C$

  $\therefore $                $\frac{dQ_{1}}{dt}=\frac{0.92\times4(100-40)}{40}$

   =4.8 cal/s