Discussion Forum

 A  block of mass m is placed on a surface with a vertical cross-section given by y=x³/6. If the coefficient of friction is 0.5, the maximum  height above  the ground at which the block can be placed without slipping is 

Answer:

Explanation:

 A block of mass m is placed on asurface with a vertical  cross-section, then 

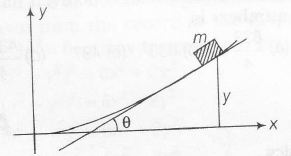
$\tan \theta=\frac{dy}{dx}\frac{d\left(\frac{x^{3}}{6}\right)}{dx}=\frac{x^{2}}{2}$

 At limiting equilibrium, we get

  $\mu=\tan\theta$

   $0.5=\frac{x^{2}}{2}$

  $\Rightarrow$           $  x^{2}=1\Rightarrow x=\pm1$

 Now, putting the value of x and y= $\frac{x^{3}}{6}$

 we get

   when x=1

  $y=\frac{(1)^{3}}{6}=\frac{1}{6}$   ,

when x=-1

   $y=\frac{(-1)^{3}}{6}=\frac{-1}{6}$  

 So, the maximum  height above the ground at which the block can be placed without slipping is 1/6 m