Discussion Forum

1)

A mass m supported by a massless string wound around a uniform hollow cylinder pf mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?

Answer:

Option B

Explanation:

 For the mass m, mg-T=ma

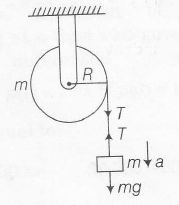
 As we know, a= Rα

 So,   $mg-T=mR\alpha$ .............(i)

 Torque about centre of pully

 $T \times R=mR^{2}\alpha$ .........(ii)

 From Eqs.(i) and (ii) , we get

          $a=\frac{g}{2}$

  Hence, the acceleration with the mass of  a body fall is   $\frac{g}{2}$