Discussion Forum

The common tangents to the circle  x²+y²=2 and the parabola  y²=8x  touch the circle at the points P, Q, and the parabola at the points  R, S. Then the area of the quadrilateral PQRS is

Answer:

Explanation:

Plan 

 (i) $y=mx+\frac{a}{m}$  is equation of tangent to the parabola y²=4ax

   (ii) A line is  atangent to circle , if distance of line from centre is equal to the radius of circle.

(iii)  Equation of chord drawn from exterior point (x₁,y₁) to a  circle/parabola is given by T=0

(iv)   Area of Trapezium= 1/2 ( sum of parallel sides) x ( distance  between them)

 Let equation  of tangent to parabola be

                    $y=mx+\frac{2}{m}$

 It also touches the circle x²+y²=2

$\therefore$     $ |\frac{2}{m\sqrt{1+m^{2}}}|=\sqrt{2}$

  $\Rightarrow$    $   m^{4}+m^{2}=2$

$\Rightarrow$    $  m^{4}+m^{2}-2=0$

$\Rightarrow$      $ (m^{2}-1)(m^{2}+2)=0$

$\Rightarrow$     $m=\pm 1,m^{2}=-2$     (m²  =-2 rejected)

 So , tangenth are y=x+2, y=-x-2, THey interset at (-2,0)

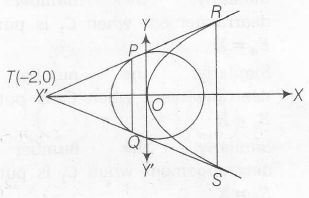
 Equation of chord PQ is, -2x=2

$\Rightarrow$        x=-1

Equation of chord RS is O =4(x-2)

$\Rightarrow$     x=2

    $\therefore$    Coordinates  of P,Q,R,S are

        P(-1,1), Q(-1,-1),R(2,4),S(2,-4) 

 Hence , are of PQRS =  $\frac{(2+8)\times3}{2}=15 $  sq.units