Discussion Forum

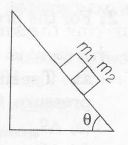
A block of mass m₁=1 kg another mass m₂= 2 kg are placed together (see figure) on an inclined plane with the angle of inclination θ. Various values of θ are given in List I.

 The coefficient of friction between the block m₁ and the plane is always zero. The coefficient of static and dynamic friction between the block m₂ and the plane are equal to   $\mu$ =0.3

 In List II expressions for the frictions on the block, m₂ are given. Match the correct expressions of the friction in list II with the angles given in List I, and choose the correct options.

 The acceleration due to gravity  is denoted by g (Useful information tan (5.5°)=0.1:

   tan (11.5°)=0.2:  tan (16.5°)=0.3]

Answer:

Explanation:

Block will not slip if

 $(m_{1}+m_{2})g\sin\theta\leq\mu m_{2}g\cos\theta$

  $\Rightarrow $   $3\sin\theta\leq\left(\frac{3}{10}\right)(2)\cos\theta$

$\tan\theta\leq\frac{1}{5}\Rightarrow\theta\leq 11.5^{0}$ 

(P)     $\theta=5^{0}$   friction is static

               $f=(m_{1}+m_{2})g\sin\theta$

(Q)     $\theta=10^{0}$   friction is static

                      $f=(m_{1}+m_{2})g\sin\theta$

(R)    $\theta=15^{0}$   friction is kinetic

       $f=\mu m_{2}g\cos\theta$

(S)     $\theta=20^{0}$   friction is kinetic 

               $f=\mu m_{2}g\cos\theta$