Discussion Forum



1)

The figure shows a circular loop of radius   $\alpha$  with two long parallel wires (numbered 1 and 2)  all in the plane of the paper. The distance of each wire from the centre of the loop is d, The loop and the wires are carrying the same current I. The  current in the loop is in the counter-clockwise direction if seen from above

2632021922_m10.JPG

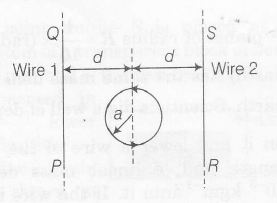
Consider d>>a, and the loop is rotated about its diameter parallel to the wire by 30° from the position shown in the figure. If the current in the wires are in the opposite directions, the torque on the loop at its new position will be (assume that the net field due to the wires  is constant over the loop)


A) $\frac{\mu_{0}l^{2}a^{2}}{d}$

B) $\frac{\mu_{0}l^{2}a^{2}}{2d}$

C) $\frac{\sqrt{3}\mu_{0}l^{2}a^{2}}{d}$

D) $\frac{\sqrt{3}\mu_{0}l^{2}a^{2}}{2d}$

Answer:

Option B

Explanation:

 Magnetic field  at mid point of two wires = 2(  magnetic field due to  one wire )

                  $=2\left[\frac{\mu_{0}}{2\pi}\frac{I}{d}\right]=\frac{\mu_{0}I}{\pi d}\otimes$

  Magnetic  moment  of loop 

 M=IA=  $I \pi a^{2}$

   Torque on loop[  = MB sin 150°

                =   $\frac{\mu_{0} I^{2} a^{2}}{2d}$