Discussion Forum

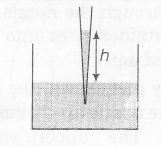
A glass capillary tube is of the shape of a truncated cone with an apex angle  $\alpha$  so that its two ends have cross-sections of different radii. When dipped in water vertically, water rises in its height h, where the radius of its cross-section in b. If the4 surface tension of water is S.  its density is ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)

Answer:

Explanation:

Using geometry 

$\frac{b}{R}=\cos(\theta+\frac{\alpha}{2})$

$\Rightarrow$   $R=\frac{b}{\cos(\theta+\frac{\alpha}{2})}$

  Using pressure  equation along the path MNTK

$p_{0}-\frac{2S}{R}+h\rho g=p_{0}$

 Substituting the value of R , we get 

           $h=\frac{2S}{R\rho g}$

         $=\frac{2S}{b\rho g}\cos(\theta+\frac{\alpha}{2})$