Discussion Forum

For a point P in the plane, let d₁(P)   and d₂(P)  be the distances of the point P from the lines x-y=0 and x+y=0, respectively. The area of the region R consisting of all points P lying  in the first quadrant  of the plane and satisfying   $2\leq d_{1}(P)+d_{2}(P)\leq 4.$   is   

Answer:

Explanation:

Plan Distance of a point (x₁,y₁) from  ax+bx+c=0 is given by

 $|\frac{ax_{1}+by_{1}+c}{\sqrt{a^{2}+b^{2}}}|$

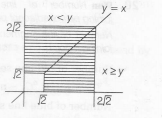
Let P(x,y)  is the point in first quadrant.

 Now,   $2\leq |\frac{x-y}{\sqrt{2}}|+|\frac{x+y}{\sqrt{2}}|\leq 4$

 $2\sqrt{2}\leq |x-y|+|x+y|\leq4\sqrt{2}$

 Case I    $x \geq y$

    $2\sqrt{2}\leq (x-y)+(x+y)\leq4\sqrt{2}$

    $\Rightarrow$     $x \in (\sqrt{2},2\sqrt{2})$

Case II     x<y

$2\sqrt{2}\leq y-x+(x+y)\leq4\sqrt{2}$

  $y \in (\sqrt{2},2\sqrt{2})$

 $\Rightarrow$       $A=(2\sqrt{2})^{2}-(\sqrt{2})^{2}=6$