Discussion Forum

From  a point  $P(\lambda,\lambda,\lambda)$  perpendicular PQ and PR are drawn  respectively on the  lines y=x, z=1 and y=-x, z=-1. If P is such that  $\angle QPR$    is a right angle , then the possible value(s) of   $\lambda$  is(are)

Answer:

Explanation:

Plan (i) Direction ratios of a line joining two points  $(x_{1},y_{1},z_{1})$  and   $(x_{2},y_{2},z_{2})$  are 

 $x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1}$

(ii) If the two lines with direction ratios a₁,b₁, c₁ ; a₂,b₂,c₂ are perpendicular , then 

a₁a₂+b₁b₂+c1c₂=0

Line L₁  given by  y=x ;z=1 can be expressed

     $L_{1}:\frac{x}{1}=\frac{y}{1}=\frac{z-1}{0}$

$\frac{x}{1}=\frac{y}{1}=\frac{z-1}{0}=\alpha$

   $\Rightarrow$             $x=\alpha,y=\alpha,z=1$

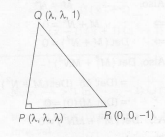
Let the coordinates od Q on L₁ be   $(\alpha,\alpha,1)$

Line L₂ Given by y=-x , z=-1 can be expressed as 

 $L_{2}:\frac{x}{1}=\frac{y}{-1}=\frac{z+1}{0}$

$\frac{x}{1}=\frac{y}{-1}=\frac{z+1}{0}=\beta$               (say)

 $\Rightarrow$       $x=\beta,y=-\beta,z=-1$

 Let the coordinates  of R on L₂  be ($ \beta$, -$\beta$, -1)

  Direction ratios of PQ are   $\lambda-\alpha,\lambda-\alpha,\lambda-1$

 Now PQ  $\bot$ L₁

$\therefore$          $1 (\lambda-\alpha)+1(\lambda-\alpha)+0.(\lambda-1)=0$

$\Rightarrow$        $ \lambda=\alpha$

$\therefore$     Q ( $\lambda$,  $\lambda$,1)

   direction ratio of PR are

             $\lambda-\beta,\lambda+\beta,\lambda+1$

  Now,    PR  $\bot$ L₂

           $\therefore$           $ 1(\lambda-\beta)+(-1)(\lambda+\beta)+0(\lambda+1)=0$

                                  $\lambda-\beta-\lambda-\beta=0$

          $\Rightarrow$            $ \beta=0$

$\therefore$     R(0,0,-1)

Now , as   $\angle QPR= 90^{0}$

   [ as a₁a₂+b₁b₂+c₁c₂ =0,

if two lines with DR'S a₁,b₁,c₁:a₂:b₂:c₂ are perpendicular)

$\therefore$    $(\lambda-\lambda)(\lambda-0)+(\lambda-\lambda)(\lambda-0)+(\lambda-1)((\lambda+1)=0$

  $\Rightarrow$     $ (\lambda-1)(\lambda+1)=0$

$\Rightarrow$    $\lambda=1 $    or $\lambda=-1 $

$\lambda=1 $   , rejected as P  and Q are different points

  $\Rightarrow$   $ \lambda$=-1