Discussion Forum

 Two parallel wires in the plane of the paper are distance X₀ apart. A point charge is moving with speed u between and wires in the same plane at a distance X₁ from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is R₁. In contrast, if the currents in the two wires have directions opposite to each other, the radius of curvature of the path is R₂. If   $\frac{X_{0}}{X_{1}}=3$ , and value of R₁/R₂ is

Answer:

Explanation:

$B_{2}=\frac{\mu_{0}I}{2\pi x_{1}}+\frac{\mu_{0}I}{2\pi(x_{0}-x_{1})}$

        { when  currents are in opposite directions)

$B_{1}=\frac{\mu_{0}I}{2\pi x_{1}}-\frac{\mu_{0}I}{2\pi(x_{0}-x_{1})}$

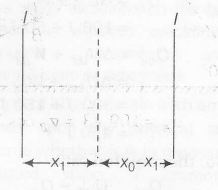
(when currents are in same direction)

Subtituting $x_{1}=\frac{x_{0}}{3}$ as \left(\frac{x_{0}}{x_{1}}\right)

$B_{1}=\frac{3\mu_{0}I}{2\pi x_{0}}-\frac{3\mu_{0}I}{4\pi x_{0}}=\frac{3\mu_{0}I}{4\pi x_{0}}$

    $R_{1}=\frac{mv}{qB_{1}} $   and  $ B_{2}= \frac{9\mu_{0}I}{4\pi x_{0}}$

 $R_{2}=\frac{mv}{qB_{2}} $

$\frac{R_{1}}{R_{2}}=\frac{B_{2}}{B_{1}}=\frac{9}{3}=3$